How will the desired centripetal force be set?
1. How will the desired centripetal force be set?
A. By choosing a value for the hanging mass.
B. By measuring the velocity, radius, and mass of the test mass.
C. The centripetal force will not be set in this experiment.
D. By measuring the acceleration and mass of the test mass.
Elevate Your Writing with Our Free Writing Tools!
Did you know that we provide a free essay and speech generator, plagiarism checker, summarizer, paraphraser, and other writing tools for free?
Access Free Writing ToolsAnswer; A. By choosing a value for the hanging mass.
2. A particle in uniform circular motion requires a net force acting in what direction?
A. Upward.
B. Towards the center of the circle.
C. Downward
D. Opposite the direction of the velocity.
E. Away from the center of the circle.
F. In the direction of velocity.
Answer; B. Towards the center of the circle.
3. The centripetal force acting on a particle is given by F = mv2/r. If the centripetal force and mass are kept constant, increasing the radius of the particle will mean that the particle’s velocity must decrease.
A. True
B. False
Answer; B. False
4. While the platform is rotating, the hanging mass remains attached to the test mass and is not removed from the platform.
A. True
B. False
Answer; B. False
Practice Problems
1. The moon revolves around the Earth once every 28 days. The mass of the moon is 7.35 x 1022 kg, while the mass of the Earth is 5.97 x 1024 kg and the average distance between their centers of mass is 384,400 km. What is the average velocity of the moon in its orbit?
Solution
The radius of the car’s path can be calculated as follows:
- Fc = mv2 / r
- Gme mm / r2 = mm v2 / r
- Gme / r = v
- v= square root ((6.67×10-11 ) (5.97 x 1024) / (384,400,000))
- v = 1018 m/s
2. A car moves in a circular path at 20 m/s. The coefficient of friction between the tires and the pavement is 0.5. What is the radius of the car’s path?
The radius of the car’s path can be calculated as follows:
- Fc = mv2 / r
- μ N = mv2 / r
- μ mg = mv2 / r
- μ g = v2 / r
- r = v2 /(μ g)
- r = 202 / (0.5)(9.8)
- r = 82 m
What is Centripetal Force?
Tie a bucket, fill it halfway with water and spin it around a vertical or horizontal circle. You will notice that the bucket could spin if you can continue rotating and pulling it towards you.
But what keeps the bucket constantly moving in a circular motion? Centripetal force!
But what exactly is this force?! The centripetal force keeps a body moving along a circular path toward the rotation’s center.
“Centripetal,” in this case, is not a type of force. Instead, it’s an adjective to describe the direction of the force as ‘towards the center. So, centripetal suggests any force that keeps objects in a circular path of motion by pulling them towards the center.
According to Isaac Newton’s second law of motion, force makes an object move in a given direction unless acted upon by another external force. Likewise, the centripetal force of an object moves it along a circle and acts toward the center.
Think of any rotating object, and you’ll see the practical application of the “center-seeking” centripetal force. For instance, the sun’s gravitational force holds the earth, and all the planets orbit around it. In the case of the bucket, the string pulls the water bucket towards the center.
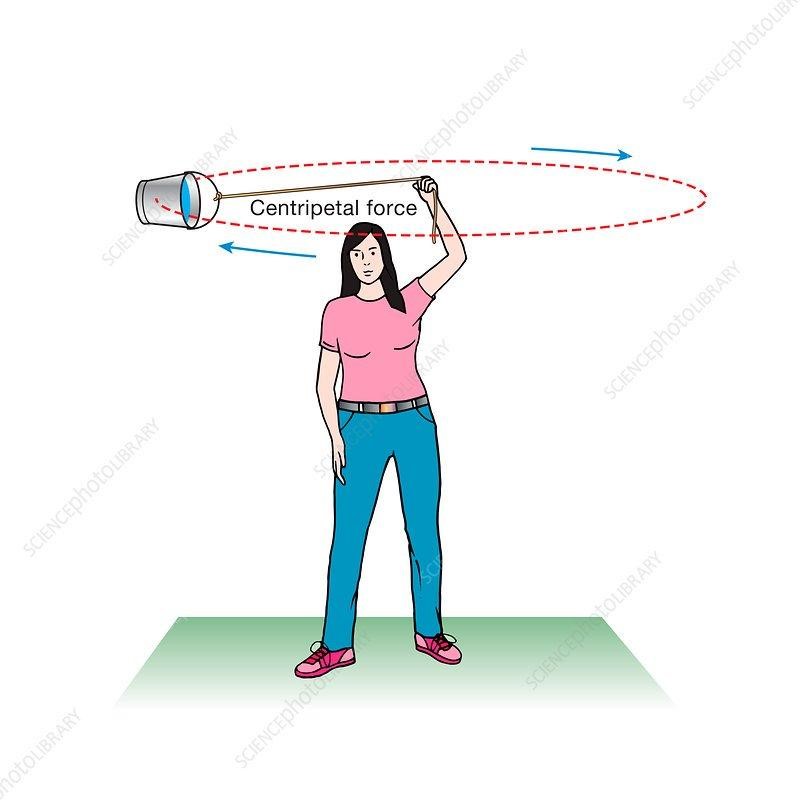
This post guides you on everything you need to know about the force acting on objects that move along curvilinear motions.
Centripetal Force Units
And which is the unit that measures centripetal force? The SI unit for measuring force is Newton (N), while the CGS unit is the dyne, and centripetal force is no exception.
The units and dimensions that measure centripetal force define how this takes place. For instance, the force acts radially on any particle or object moving in a circular motion toward the center.

Force is therefore influenced by the radius r of the circular path formed by the object, the object’s mass m, and the velocity v at which the object moves.
How to Calculate Centripetal Force?
Calculating the centripetal force is easy if you understand the fundamental mechanisms that keep the object in motion. First, the centripetal force acts on objects moving along curvilinear lines, and it’s directed to the axis of the rotation or center of the curvature. So, the force acts perpendicularly to the displacement of the object.
Newton says that every moving object remains in the state and direction of motion unless it is forced to stop or change direction by another force. If a centripetal force acts on an object moving in a straight line, it directs it toward the center of the circular path. The objects’ velocity then follows the circular path.
So, centripetal force is the external force that makes the object move in a circular path instead of following a straight line. For instance, when spinning the bucket of water, the string acts as the perpendicular displacement, basically representing the centripetal force.
If you removed the centripetal force by breaking the string during the spinning, the bucket would fly away along the circle’s tangent.
Therefore, the centripetal force overcomes all this through three factors; the velocity of the object, the object’s displacement from the center, and the object’s mass.
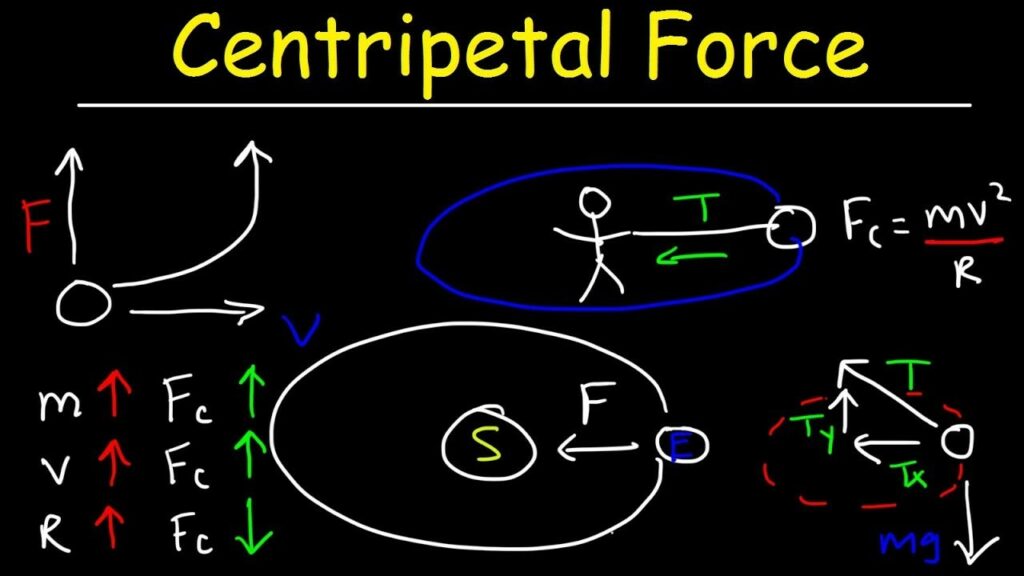
As long as you have the mass (m) of the object, its displacement from the center r, and the tangential velocity (v), you can calculate the centripetal force Fc.
Centripetal force, F = mass of the object, m x Tangential velocity squared, V² / radius or object’s displacement, r
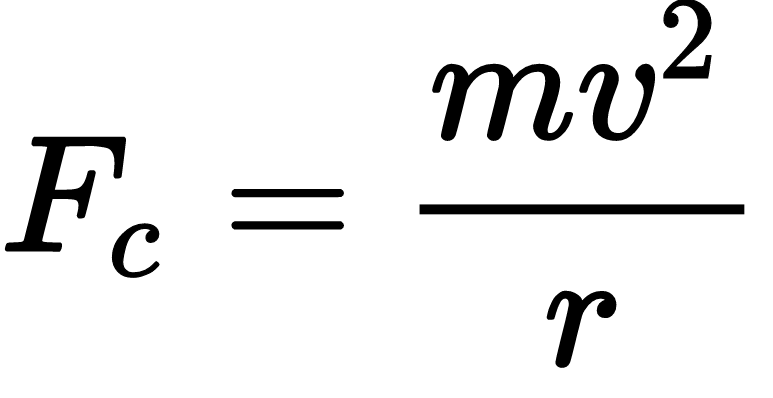
v²/r is acceleration because any object moving along a curved path is basically in acceleration with force directed toward the center of the circle formed by the path.
In application, this formula proves that the centripetal force is directly proportional to the square of tangential velocity. So, if you double the speed of a moving object, you will need four times the centripetal force to keep it in a circular motion.
For example, increasing a car’s speed on a curve is dangerous because the frictional force caused by the tires and the road’s surface may not be enough to overcome the resulting centrifugal force. This could easily lead to unexpected skidding or drifting and result in an accident.
The centripetal force formula applies to any data values. But, it assumes that no additional forces are applying to the moving object.
What is the Difference Between Centripetal and Centrifugal Force?
Many students confuse centripetal forces with centrifugal forces, but they differ. First, the centripetal force is the force that keeps things in circular motions. It pulls objects moving along circular paths towards the center.
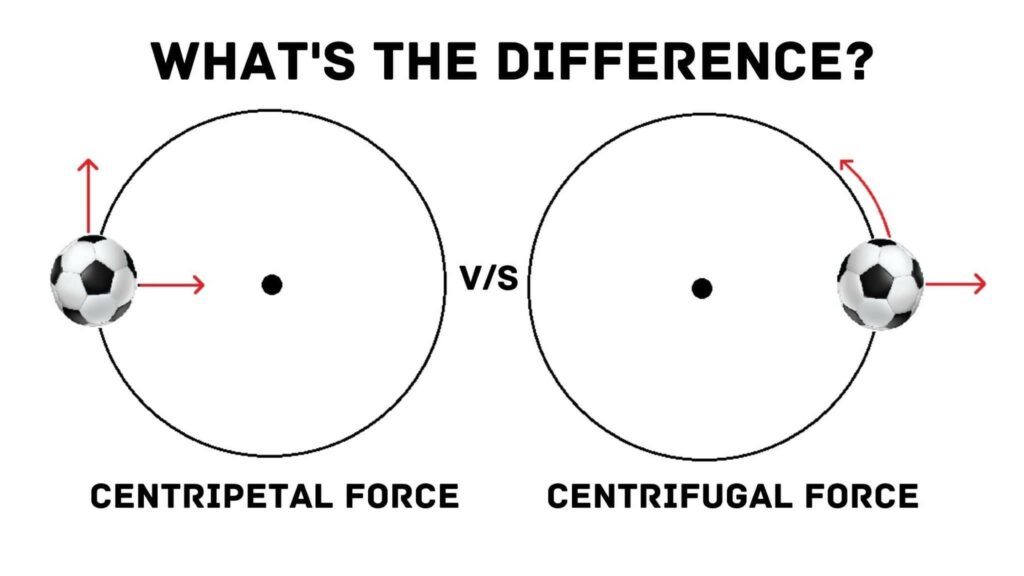
However, the centrifugal force isn’t an actual force. Instead, it is the inertia caused by the centripetal force. Newton’s Third Law says every force must have an equally opposite force. So, in simple terms, centrifugal force is the reaction to the centripetal force’s action.
The centripetal force acts towards the center of the rotating object, but the centrifugal force reacts by taking the objects away from the center.
While the centripetal force pulls the bucket towards your hands, the centrifugal force will pull the water away from you. Therefore, the centrifugal force prevents the water from spilling out. And the centripetal keeps the bucket spinning around.
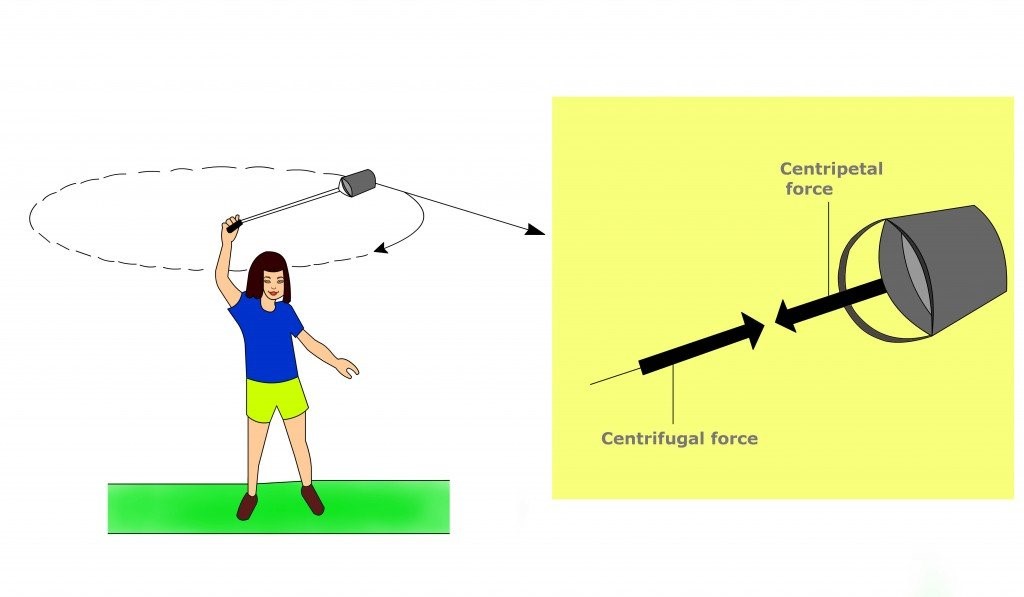
You must exert enough centripetal force to keep the bucket rotating around you. The speed at which your bucket rotates depends directly on the centripetal force you apply.
Likewise, little centrifugal force will make the water spill over eventually. So, you have to maintain a centripetal force that attracts an equal opposite centrifugal force that’s enough to keep your water firmly in the bucket.
Examples:
Tie a bucket, fill it halfway with water and spin it around a vertical or horizontal circle. You will notice that the water stays calmly in the bucket.
But what exactly keeps the water unmoved in the pail? Centrifugal force!
And what keeps the bucket constantly moving in a circular motion? Centripetal force!
Watch kids hold on tightly at their seats during a merry-go-round train.
What makes it harder for them to hold on as the wheel turns faster and faster? Again, centrifugal force!
What keeps the seats moving around the merry-go-round train? Centripetal force!
How Does The Centripetal Force Affect Circular Motion?
As aforementioned, it is the nature of moving objects to stick to linear trajectories unless acted upon by external forces. The centripetal force is center-seeking, which pulls moving objects toward the center. So, it forces things to keep moving around the circumference. But how does this influence circular motion?
First, the velocity keeps changing even when an object moves around the circle’s perimeter at a constant speed. For an object to move in a circular motion, it must keep changing its direction and, thus, its velocity.

Therefore, the constant change in velocity means an acceleration directed toward the circle’s center. According to Newton’s second law, the object experiences acceleration because it is also experiencing a net force. The net force’s direction is centripetal, and so is acceleration.
To keep the particle in motion at a constant speed along a circular path, the acceleration toward the center requires a force acting along the radius.This is known as the centripetal force requirement.
And while the object’s speed remains constant, the centripetal force affects circular motion by constantly changing the trajectory direction.
What Causes Centripetal Force?
Objects moving in circular orbits experience centripetal forces radially toward the center of the circular path. But what exactly causes the centripetal force?
Newton’s first law of motion explicitly states that all objects would ideally stay at their initial state of motion unless external forces act upon them. In such a case, the object would follow the direction guided by the force.
Take the case of a car speeding along the street in a straight line. The car would remain in that straight line unless acted upon by friction and gravity. If the vehicle finds a corner or roundabout and tries to turn, then centripetal forces keep the car from skidding.
The turning invites a new force- the centripetal force- to act radially on the car, pulling it inwards towards the center of the circular curve that the road’s curve would form. So, the new centripetal force acting along the radius changes the car’s trajectory from linear to circular. In this case, the friction between the car’s tires and the road’s surface brings about the centripetal force.
The earth and other planets move in circular orbits around the sun. The sun’s gravitational pull towards its center causes the centripetal force.
In the water bucket’s case, the string represents the radial force you apply to pull the bucket towards you. And pulling the bucket towards you causes the centripetal force.
An electron keeps moving around the nucleus of an atom. The electrostatic force between the negatively charged electron and the positively charged protons at the center provides the centripetal force.

Special offer! Get 20% discount on your first order. Promo code: SAVE20