Calculus Concepts You Need to Know

Published by Boni on March 8, 2021March 8, 2021

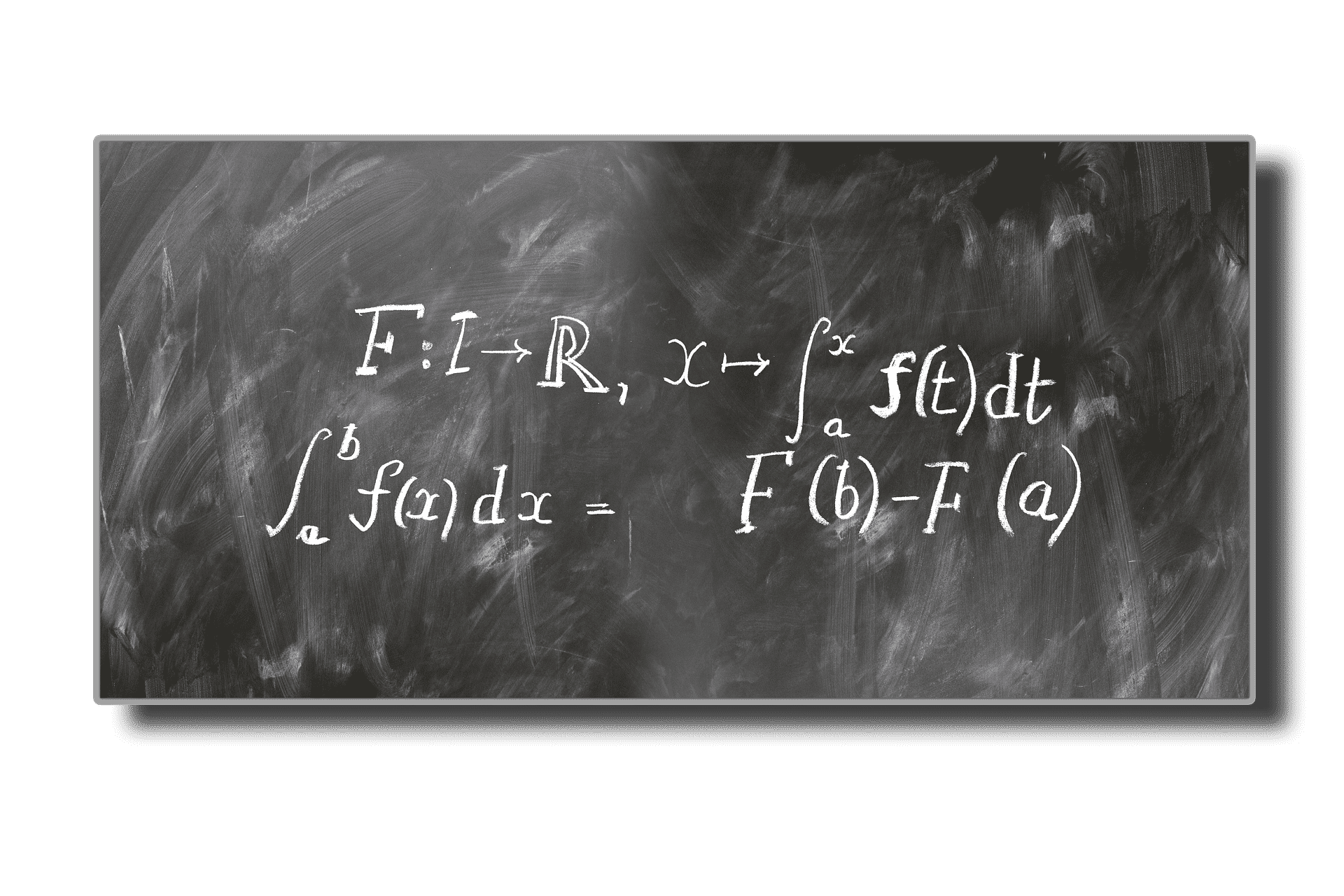
For most learners of calculus, the best way they would describe their relationship with the subject is Love/Hate. Do you remember the Darwin’s Theory of Evolution? By the time you are done with that topic in school, you inevitably begin to see the world as one large playground where every player is aiming for their own survival; it suddenly makes sense to you why some germs develop resistance to some type of drugs or why a diet that comprises fat and sugar is tastier than the alternative.

Well, a study and mastery of calculus brings the same level of enlightenment. Have you ever stopped to ponder on the various formulas of circles and spheres? Ideally, we are talking about the same structure only that we look at it from different angles. Instead of learning to find the circumference and area of these related shapes independently, finding the co-relation and application makes learning much more fun.  In the spirit of survival, it makes sense to prepare for calculus exams by asking to pay someone to do my statistics homework and get professional help.

Most Important Calculus Concepts You Must Know

For a long time, math in general has been perceived to be a hard subject that only the brightest of the intelligent minds can manage to do; no wonder some people will use math performance to gauge your school work ability. The fact that those who take math in college happen to grasp it at some level means that math and calculus specifically is indeed not hard.

Actually, most students keep asking themselves how they can get an A in calculus? It is very simple since all you have to do is master these three fundamental concepts;

1. Limits

This is probably the first class you will be learning in your calculus course. When asked to find the limit of a function, what the examiner really wants is to establish the next value of the function as it moves towards a certain mark. If you are given this problem for instance, find the limit of function f (x) =3x+1 as x nears 2 is the same to being asked to find the number that the above formula approaches as the value of x nears 2. Get to know what chain rule is.

If asked to find the limit of a function at a certain point, it means that the answer you should give should be the value of the said function at that particular point. The only exception to this rule is when p is equal to infinity or the function at the point stated has no value.

The bottom line is that limits are a crucial subject in calculus because they are the only approach to use when estimating the value of an infinite series.

2. Derivatives

Do you remember the slope concept in algebra? The inclination of the line is able to tell you the rate with which y changes in relation to x and vice versa. In calculus, this concept goes deeper to cover similar changes but in graphs where the line is not straight. In short, a derivative allows you to calculate the slope or gradient in curves.

It is important to remember that the gradient of these curved graphs is different at ever point. This means that for every derivative, the function has a variable in it. For example, the rate of change of the function f(x) =x2 is equal to 2x. So, if you were to be asked to find the slope at a point where x=3, the answer would be 6.

3. Integrals

In simple terms, an integral is the area on a graph under a line or curve. As an example, think of a question that asks you to integrate a function y=3, a horizontal line over an interval of x= (0, 2). This problem would be the same if the question asked you to find the area of a rectangle with a height of 3 and a width of 2 (the origin of the graph would mark the south west point of such a rectangle.) actually, this is such an easy example, not the kind that calculus would be used for.

In the real sense, the areas under graphs encountered in calculus are rectangles with an odd top profile. The height for each of these rectangles is f(x) width id dx. In most cases, dx is constant in all the rectangles in a graph. So, to find the area of a single rectangle, the formula would be [dx] [f(x (p))] at the point where x=p. the integral in this case would calculate the sum of the mini rectangles within the main area up to infinity.

Does this sound complicated? It does for most people at first until you understand that this is the most accurate way of calculating the area with weird shaped edges as opposed to the straight lines we are used to. In time you will understand that the opposite of integration of a function is deriving a function and the reverse is true.

Get insights on IB Math IA topics – tips and ideas.

Concepts Recap

There is no doubt that calculus is a tricky subject and many of those who study the subject will admit that they did not understand much from the first lesson. The most important point is to carry away something from every lesson. Let us start with what we have covered in the above description for instance. Three points stand out;

• A limit will give you the prediction at a certain point for a given value
• Derivatives will give you an insight into how much a function changes at a given point
• Integrals are the opposite of derivatives and are used to calculate the areas of odd shaped spaces.

With the internet and smartphone revolution, calculus homework can be accessed from various parts of the globe. You might have noticed already that calculus borrows concepts from previous math topics. There is therefore no magic wand for understanding and passing calculus; just understand the previous lesson thoroughly and you have a strong foundation for the current and subsequent classes.

It is also important to pay attention to your calculus homework as this will form the basis of your exams. You can as well use our reliable Calculus homework help service and save yourself time that can be used to concentrate on other  productive tasks or used to attend to the social aspects of your life.

Special offer! Get 20% discount on your first order. Promo code: SAVE20