What is the Chain Rule?

The chain rule is an essential concept in calculus, which is used to calculate the derivative of a composite function. A composite function is a function that contains two or more functions joined inside one another. For example, if we have a function f(x) = sin(x^2), we can think of it as a composition of two functions: g(x) = x^2 and h(x) = sin(x).

The chain rule formula states that dy/dx = dy/du * du/dx.  That is, differentiate the outer function while keeping the inner function the same then multiply this by the derivative of the inner function. The chain rule formula is dy/dx= dy/du * du/dx where u is a function of 𝑥 [u = g(x)] and y is a function of u [y = f(u)].

Additionally, the chain rule can as well be written in function notation as F'(𝑥) = f'(g (𝑥)).g'(𝑥),

where;

• F (𝑥) = f [g(𝑥)]
• g (𝑥) is the inner function and f(𝑥) is the outer function.

In order to use the chain rule, the inner function must be kept constant while determining the derivative of the outer function, which must then be multiplied by the derivative of the inner function.

Certain guidelines must be followed in order to apply the chain rule: The function has to be a combination of at least two other functions and the functions must be distinct from one another.

How to do the Chain Rule

The chain rule allows you to break down the functions into their component parts and find their derivatives with regard to their independent variable. In this article, we will explain how to use the chain rule to find the derivative of composite functions.

Get tips and ideas on IB Math topics.

Step One: Differentiate the outer function, keeping the inner function the same.

This is the first step while using the chain rule. For instance, differentiate (5𝑥 – 2) ^4 using the chain rule. In this case, 5x-2 is the inner function and () ^4 is the outer function.  Therefore, we differentiate the outer function as x4.

We differentiate x4 to 5×4 to have () ^4 which is differentiated as 4() ^5.  We then keep the inner function of 5x-2, so we will have 4(5x – 2) ^5

In the end, we will have 5x-2 inside the brackets and not x, which then takes us to the next step.

Step Two: Multiply this by the derivative of the inner function

Picking from 4(5x – 2) ^5, the next thing is to multiply this by the derivative of the inner function.

Where the inner function is 5x – 2.

Therefore, we differentiate 5x – 2 to get 5 and thus we multiply the result of 4(5x – 2) ^5.

We get the answer of f'(𝑥) = 20(5𝑥 – 2) ^5.

For example; differentiate f'(𝑥) = (5𝑥 – 2) ^5.                 

dy/dx = (differentiate the outer function and keep the inner part the same) (differentiate the inner function)

f(𝑥) = (5𝑥 – 2) ^5.

So f'(𝑥) = 20(5𝑥 – 2) ^5. 5 (5).

And you get the answer as f’(𝑥) = 20(5𝑥 – 2) ^5.

Explore how to learn calculus in 7 simple steps.

Chain Rule with Trigonometry

The chain rule is employed to distinguish between trigonometric functions that contain other functions. Multiply the trigonometric function by the derivative of the inner function after differentiating it while maintaining the inner function constant.

It may be helpful to utilize the following guidelines for differentiating the trigonometric functions sin(x), cos(x), and tan(x) in this situation:

Derivate of Trigonometry Functions

          F(x) = Sin(x) 

For instance;

1. Differentiate cos(3𝑥) using the chain rule.

cos(3𝑥) can be written as;

• Inner function of 3𝑥
• Outer function of cos().

The first step is to differentiate the outer function, keeping the inner function the same.

cos(𝑥) differentiates to -sin(𝑥) and so, keeping the inner function as 3𝑥 rather than 𝑥, we get -sin(3𝑥).

Then multiply it by the derivative of the inner function

Where the inner function is 3𝑥 and its derivative is 3. We then multiply -sin(3𝑥) by 3 to get;

f'(x) = -3sin(3𝑥).

2. Differentiate f(x) = cos(2x) using the chain rule.

The Chain Rule with Exponential Functions

In exponential functions, the variable is expressed as an exponent. The chain rule derivative of y = e𝑥 is dy/d𝑥 = e𝑥 and after using the chain rule, the derivative of y = ef(𝑥) is dy/d𝑥 = f'(𝑥).ef(𝑥). Then differentiate the power of e and then multiply it by the original function.

Here is the formula, If y=

The Chain Rule with Logs

We first need to understand how to define and differentiate functions in order to use the chain rule with logs. Therefore, chain rule states that for y = ln(u), dy/d𝑥 = 1/u × du/d𝑥.  Differentiate the inner function and then divide this by the inner function.

Example; differentiate Y = In(x^2 + 3x)

Applying the Chain Rule with Three Functions

Chain rule can be used for the composition of three functions. For instance, If y(𝑥) = h(g(f(x))), then y'(𝑥) = f'(𝑥) . g'(f(𝑥)) . h'(g(f(𝑥))). H, therefore, it is easy to use the chain rule twice to differentiate three functions.

For Eexample;

Differentiate f(𝑥) = sin^2(5𝑥).

We now have the composition of 3 functions which are;

• Innermost function is 5𝑥.
• Acting on the 5𝑥 is the sin function
• The sin function is raised to the power of 2

F(𝑥) = [sin(5𝑥)]^2

F'(𝑥) = 2[sin(5𝑥)] . 5cos(5𝑥)

F'(𝑥) = 10 sin(5𝑥) cos(5𝑥)

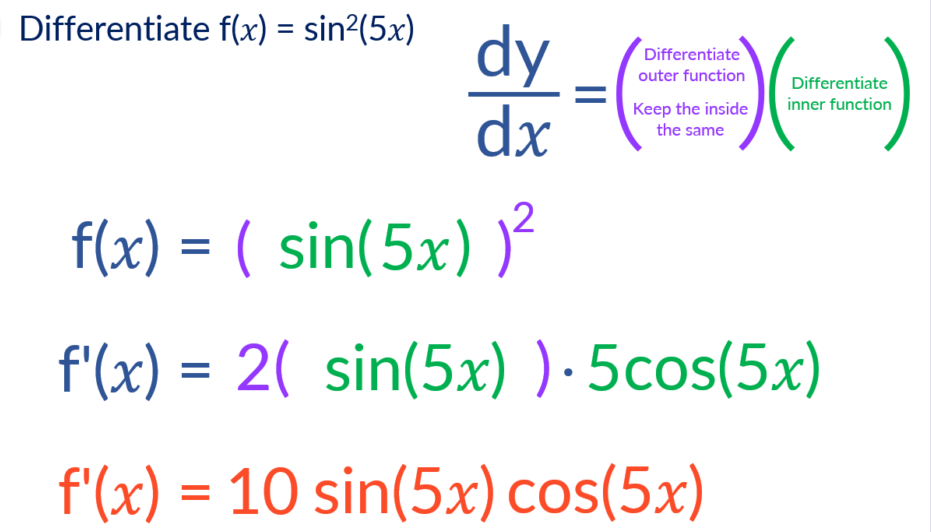
Chain Rule Examples with Solutions               

If you have a challenging task on Chain rule, seek online calculus homework help from our team of professionals and guarantee yourself an A+ grade. . Here are some of the examples you can look at to differentiate different functions.

Function	Calculation                                  Derivatives
f(𝑥) = (5𝑥 + 1)3	3 × (5𝑥 + 1)2 × 5                          f'(𝑥) = 15(5𝑥 + 1)2
f(𝑥) = sin(5𝑥)	cos(5𝑥) × 5                                  f'(𝑥) = 5cos(5𝑥)
f(𝑥) = cos(10𝑥)	-sin(10𝑥) × 10                              f'(𝑥) = -10sin(10𝑥)
f(𝑥) = -3tan(2𝑥)	-3sec2(2𝑥) × 2                             f'(𝑥) = -6 sec2(2𝑥)
f(𝑥) = 10e4𝑥	10e4𝑥 × 4                                     f'(𝑥) = 40e4𝑥
f(𝑥) = ln(𝑥3)	1/(𝑥3) × 3𝑥2 = (3𝑥2)/(𝑥3)              f'(𝑥) = 3/𝑥

When to Use the Chain Rule

The chain rule is an important idea in calculus that is used to distinguish composite functions. When separating functions that are not in a simple form or dealing with functions that contain several nested functions, it is crucial. Success in calculus and related disciplines depends on being able to employ the chain rule when it is appropriate. The table below shows when to use and not to use the chain rule.

Example	Should I use the chain rule?	Why?
y = (3𝑥+2)5	Yes	The inner function is 3𝑥+2 and the outer function is 𝑥5.
y = 𝑥5	No	There is only one function 𝑥5. It can be differentiated directly.
y = (𝑥+3) sin(𝑥)	No	It is the product of two functions. Use the product rule.
y = sin(2𝑥+1)	Yes	The inner function is 2𝑥+1 and the outer function is sin(𝑥)
y = (𝑥+5)/(3x+5)	No	It is a fraction with a function for a numerator and denominator. Use the quotient rule.
y = ln(𝑥4-𝑥)	Yes	The inner function is 𝑥4-𝑥. The outer function is ln(𝑥).
y = e2𝑥	Yes	The inner function is 2𝑥 and the outer function is e𝑥.

Chain Rule Proof

Applying the derivative’s limit definition and engaging in algebraic manipulation is required for the chain rule’s proof. Students can better understand the fundamental ideas behind the chain rule and develop their calculus problem-solving skills by comprehending how the chain rule is proved. 

Therefore, to prove the chain rule, check dy/dx as a limit of Δy/Δ𝑥 as 𝑥 tends to zero. This can be written as limits of Δy/Δu × Δu/Δ𝑥. Assessing these limits as 𝑥 and u tend to zero, you develop the chain rule as dy/d𝑥 = dy/du × dy/d𝑥. You need to have the following to prove the chain rule;

• Write dy/d𝑥 as a limit of Δy/Δ𝑥 as 𝑥 tends to zero.
• Write the limit of Δy/Δ𝑥 as Δy/Δu × Δu/Δ𝑥. Δu is a number so this can be done.
• Separate the limit into 2 limits of Δy/Δu and Δu/Δ𝑥.
• As Δ𝑥 tends to 0, so does Δu.
• Then assess both limits to get dy/d𝑥 = dy/du × du/d𝑥.

Special offer! Get 20% discount on your first order. Promo code: SAVE20